When you write an arithmetic expression such as B * C, the form of theexpression provides you with information so that you can interpret itcorrectly. In this case we know that the variable B is being multipliedby the variable C since the multiplication operator * appears betweenthem in the expression. This type of notation is referred to asinfix since the operator is in between the two operands that it isworking on.

Consider another infix example, A + B * C. The operators + and * stillappear between the operands, but there is a problem. Which operands dothey work on? Does the + work on A and B or does the * take B and C?The expression seems ambiguous.

Jan 03, 2015  Suppose we wanted to convert a mathematical expression like 3^4+(11-(3.2))/2 into a reverse polish notation expression to evaluate the answer. This is called an infix expression. To convert it(to be able to evaluate the expression as well), we will use shunting yard algorithm. This algorithm is stack based and also includes an output list. . This is 'Infix'notation. VKS-LEARNING HUB Prefix Notation. Instead of saying 'A plus B', we could say 'add A,B ' and write + A B. 'Multiply A,B' would be written. A B. This is Prefixnotation. VKS-LEARNING HUB Postfix Notation. Another alternative is to put the operators after the operands as in A B + and A B. This is.

In fact, you have been reading and writing these types of expressionsfor a long time and they do not cause you any problem. The reason forthis is that you know something about the operators + and *. Eachoperator has a precedence level. Operators of higher precedence areused before operators of lower precedence. The only thing that canchange that order is the presence of parentheses. The precedence orderfor arithmetic operators places multiplication and division aboveaddition and subtraction. If two operators of equal precedence appear,then a left-to-right ordering or associativity is used.

Let’s interpret the troublesome expression A + B * C using operatorprecedence. B and C are multiplied first, and A is then added to thatresult. (A + B) * C would force the addition of A and B to be donefirst before the multiplication. In expression A + B + C, by precedence(via associativity), the leftmost + would be done first.

Although all this may be obvious to you, remember that computers need toknow exactly what operators to perform and in what order. One way towrite an expression that guarantees there will be no confusion withrespect to the order of operations is to create what is called a fullyparenthesized expression. This type of expression uses one pair ofparentheses for each operator. The parentheses dictate the order ofoperations; there is no ambiguity. There is also no need to remember anyprecedence rules.

The expression A + B * C + D can be rewritten as ((A + (B * C)) + D)to show that the multiplication happens first, followed by the leftmostaddition. A + B + C + D can be written as (((A + B) + C) + D) since theaddition operations associate from left to right.

Disney magic artist 3d download free. The price may be the seller's own price elsewhere or another seller's price. The 'off' amount and percentage simply signifies the calculated difference between the seller-provided price for the item elsewhere and the seller's price on eBay.

There are two other very important expression formats that may not seemobvious to you at first. Consider the infix expression A + B. What wouldhappen if we moved the operator before the two operands? The resultingexpression would be + A B. Likewise, we could move the operator to theend. We would get A B +. These look a bit strange.

These changes to the position of the operator with respect to theoperands create two new expression formats, prefix and postfix.Prefix expression notation requires that all operators precede the twooperands that they work on. Postfix, on the other hand, requires thatits operators come after the corresponding operands. A few more examplesshould help to make this a bit clearer (see Table 2).

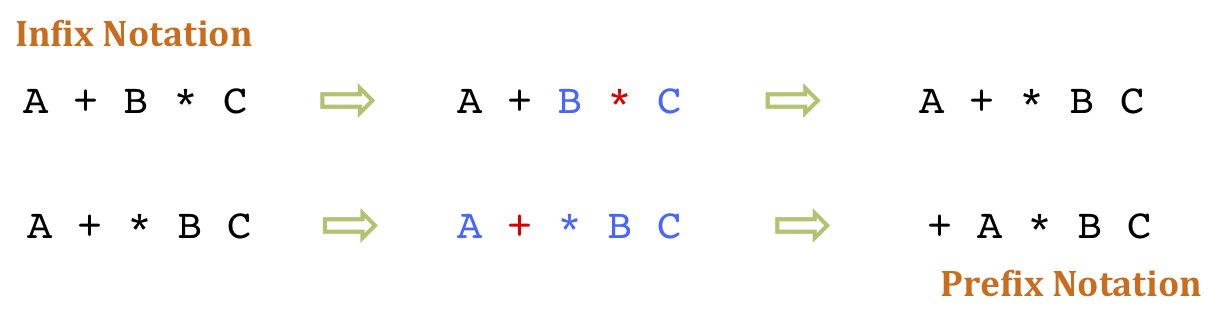
A + B * C would be written as + A * B C in prefix. The multiplicationoperator comes immediately before the operands B and C, denoting that *has precedence over +. The addition operator then appears before the Aand the result of the multiplication.

In postfix, the expression would be A B C * +. Again, the order ofoperations is preserved since the * appears immediately after the B andthe C, denoting that * has precedence, with + coming after. Althoughthe operators moved and now appear either before or after theirrespective operands, the order of the operands stayed exactly the samerelative to one another.

Now consider the infix expression (A + B) * C. Recall that in thiscase, infix requires the parentheses to force the performance of theaddition before the multiplication. However, when A + B was written inprefix, the addition operator was simply moved before the operands, + AB. The result of this operation becomes the first operand for themultiplication. The multiplication operator is moved in front of theentire expression, giving us * + A B C. Likewise, in postfix A B +forces the addition to happen first. The multiplication can be done tothat result and the remaining operand C. The proper postfix expressionis then A B + C *.

Consider these three expressions again (see Table 3).Something very important has happened. Where did the parentheses go? Whydon’t we need them in prefix and postfix? The answer is that theoperators are no longer ambiguous with respect to the operands that theywork on. Only infix notation requires the additional symbols. The orderof operations within prefix and postfix expressions is completelydetermined by the position of the operator and nothing else. In manyways, this makes infix the least desirable notation to use.

Table 4 shows some additional examples of infix expressions andthe equivalent prefix and postfix expressions. Be sure that youunderstand how they are equivalent in terms of the order of theoperations being performed.

4.9.1. Conversion of Infix Expressions to Prefix and Postfix¶

So far, we have used ad hoc methods to convert between infix expressionsand the equivalent prefix and postfix expression notations. As you mightexpect, there are algorithmic ways to perform the conversion that allowany expression of any complexity to be correctly transformed.

The first technique that we will consider uses the notion of a fullyparenthesized expression that was discussed earlier. Recall that A + B* C can be written as (A + (B * C)) to show explicitly that themultiplication has precedence over the addition. On closer observation,however, you can see that each parenthesis pair also denotes thebeginning and the end of an operand pair with the corresponding operatorin the middle.

Look at the right parenthesis in the subexpression (B * C) above. If wewere to move the multiplication symbol to that position and remove thematching left parenthesis, giving us B C *, we would in effect haveconverted the subexpression to postfix notation. If the additionoperator were also moved to its corresponding right parenthesis positionand the matching left parenthesis were removed, the complete postfixexpression would result (see Figure 6).

Figure 6: Moving Operators to the Right for Postfix Notation¶

If we do the same thing but instead of moving the symbol to the positionof the right parenthesis, we move it to the left, we get prefix notation(see Figure 7). The position of the parenthesis pair isactually a clue to the final position of the enclosed operator.

Figure 7: Moving Operators to the Left for Prefix Notation¶

So in order to convert an expression, no matter how complex, to eitherprefix or postfix notation, fully parenthesize the expression using theorder of operations. Then move the enclosed operator to the position ofeither the left or the right parenthesis depending on whether you wantprefix or postfix notation.

Here is a more complex expression: (A + B) * C - (D - E) * (F + G).Figure 8 shows the conversion to postfix and prefixnotations.

Figure 8: Converting a Complex Expression to Prefix and Postfix Notations¶

4.9.2. General Infix-to-Postfix Conversion¶

We need to develop an algorithm to convert any infix expression to apostfix expression. To do this we will look closer at the conversionprocess.

Consider once again the expression A + B * C. As shown above,A B C * + is the postfix equivalent. We have already noted that theoperands A, B, and C stay in their relative positions. It is only theoperators that change position. Let’s look again at the operators in theinfix expression. The first operator that appears from left to right is+. However, in the postfix expression, + is at the end since the nextoperator, *, has precedence over addition. The order of the operatorsin the original expression is reversed in the resulting postfixexpression.

As we process the expression, the operators have to be saved somewheresince their corresponding right operands are not seen yet. Also, theorder of these saved operators may need to be reversed due to theirprecedence. This is the case with the addition and the multiplication inthis example. Since the addition operator comes before themultiplication operator and has lower precedence, it needs to appearafter the multiplication operator is used. Because of this reversal oforder, it makes sense to consider using a stack to keep the operatorsuntil they are needed.

What about (A + B) * C? Recall that A B + C * is the postfixequivalent. Again, processing this infix expression from left to right,we see + first. In this case, when we see *, + has already been placedin the result expression because it has precedence over * by virtue ofthe parentheses. We can now start to see how the conversion algorithmwill work. When we see a left parenthesis, we will save it to denotethat another operator of high precedence will be coming. That operatorwill need to wait until the corresponding right parenthesis appears todenote its position (recall the fully parenthesized technique). Whenthat right parenthesis does appear, the operator can be popped from thestack.

As we scan the infix expression from left to right, we will use a stackto keep the operators. This will provide the reversal that we noted inthe first example. The top of the stack will always be the most recentlysaved operator. Whenever we read a new operator, we will need toconsider how that operator compares in precedence with the operators, ifany, already on the stack.

Assume the infix expression is a string of tokens delimited by spaces.The operator tokens are *, /, +, and -, along with the left and rightparentheses, ( and ). The operand tokens are the single-characteridentifiers A, B, C, and so on. The following steps will produce astring of tokens in postfix order.

1. Create an empty stack called opstack for keeping operators.Create an empty list for output.

2. Convert the input infix string to a list by using the string methodsplit.

3. Scan the token list from left to right.

   • If the token is an operand, append it to the end of the outputlist.

   • If the token is a left parenthesis, push it on the opstack.

   • If the token is a right parenthesis, pop the opstack until thecorresponding left parenthesis is removed. Append each operator tothe end of the output list.

   • If the token is an operator, *, /, +, or -, push it on theopstack. However, first remove any operators already on theopstack that have higher or equal precedence and append themto the output list.

4. When the input expression has been completely processed, check theopstack. Any operators still on the stack can be removed andappended to the end of the output list.

Figure 9 shows the conversion algorithm working on theexpression A * B + C * D. Note that the first * operator is removedupon seeing the + operator. Also, + stays on the stack when the second* occurs, since multiplication has precedence over addition. At the endof the infix expression the stack is popped twice, removing bothoperators and placing + as the last operator in the postfix expression.

Figure 9: Converting A * B + C * D to Postfix Notation¶

In order to code the algorithm in Python, we will use a dictionarycalled prec to hold the precedence values for the operators. Thisdictionary will map each operator to an integer that can be comparedagainst the precedence levels of other operators (we have arbitrarilyused the integers 3, 2, and 1). The left parenthesis will receive thelowest value possible. This way any operator that is compared against itwill have higher precedence and will be placed on top of it.Line 15 defines the operands to be any upper-case character or digit.The complete conversion function isshown in ActiveCode 1.

A few more examples of execution in the Python shell are shown below.

4.9.3. Postfix Evaluation¶

As a final stack example, we will consider the evaluation of anexpression that is already in postfix notation. In this case, a stack isagain the data structure of choice. However, as you scan the postfixexpression, it is the operands that must wait, not the operators as inthe conversion algorithm above. Another way to think about the solutionis that whenever an operator is seen on the input, the two most recentoperands will be used in the evaluation.

To see this in more detail, consider the postfix expression456*+. As you scan the expression from left to right, you firstencounter the operands 4 and 5. At this point, you are still unsure whatto do with them until you see the next symbol. Placing each on the stackensures that they are available if an operator comes next.

In this case, the next symbol is another operand. So, as before, push itand check the next symbol. Now we see an operator, *. This means thatthe two most recent operands need to be used in a multiplicationoperation. By popping the stack twice, we can get the proper operandsand then perform the multiplication (in this case getting the result30).

We can now handle this result by placing it back on the stack so that itcan be used as an operand for the later operators in the expression.When the final operator is processed, there will be only one value lefton the stack. Pop and return it as the result of the expression.Figure 10 shows the stack contents as this entire exampleexpression is being processed.

Figure 11 shows a slightly more complex example, 7 8 + 3 2+ /. There are two things to note in this example. First, the stack sizegrows, shrinks, and then grows again as the subexpressions areevaluated. Second, the division operation needs to be handled carefully.Recall that the operands in the postfix expression are in their originalorder since postfix changes only the placement of operators. When theoperands for the division are popped from the stack, they are reversed.Since division is not a commutative operator, in other words(15/5) is not the same as (5/15), we must be sure thatthe order of the operands is not switched.

Figure 11: A More Complex Example of Evaluation¶

Assume the postfix expression is a string of tokens delimited by spaces.The operators are *, /, +, and - and the operands are assumed to besingle-digit integer values. The output will be an integer result.

1. Create an empty stack called operandStack.

2. Convert the string to a list by using the string method split.

3. Scan the token list from left to right.

   • If the token is an operand, convert it from a string to an integerand push the value onto the operandStack.

   • If the token is an operator, *, /, +, or -, it will need twooperands. Pop the operandStack twice. The first pop is thesecond operand and the second pop is the first operand. Performthe arithmetic operation. Push the result back on theoperandStack.

4. When the input expression has been completely processed, the resultis on the stack. Pop the operandStack and return the value.

The complete function for the evaluation of postfix expressions is shownin ActiveCode 2. To assist with the arithmetic, a helperfunction doMath is defined that will take two operands and anoperator and then perform the proper arithmetic operation.

It is important to note that in both the postfix conversion and thepostfix evaluation programs we assumed that there were no errors in theinput expression. Using these programs as a starting point, you caneasily see how error detection and reporting can be included. We leavethis as an exercise at the end of the chapter.

Self Check

Q-1: Without using the activecode infixToPostfix function, convert the following expression to postfix 10+3*5/(16-4) .

Q-2: What is the result of evaluating the following: 1710+3*9/ ?

Q-3: Modify the infixToPostfix function so that it can convert the following expression: 5*3**(4-2). Run the function on the expression and paste the answer here:

Video: (video_Stack3)